This article explores how first-order and second-order phase transitions manifest in electronic materials and devices. We examine their theoretical foundations and practical implications, with a focus on steep-slope devices such as NC-FETs. Special attention is given to the interplay between ferroelectricity, subthreshold swing, and dynamic stability in 2D and advanced semiconductor systems.
Phase Transitions in Electronic Materials and Devices: From Thermodynamic Foundations to the Limits of Negative Capacitance FETs
Introduction
Phase transitions — whether first-order or second-order — offer a powerful lens through which we can understand complex emergent behaviors in condensed matter systems. In modern electronic devices, especially those employing two-dimensional (2D) materials and strongly correlated electron systems, these transitions govern dramatic changes in transport, dielectric, and structural properties.
This article approaches the problem of device behavior from a thermodynamic phase transition perspective, starting with fundamental concepts and extending to field-effect transistors (FETs), with a particular focus on the controversial Negative Capacitance FET (NC-FET). We combine theory, analytical modeling, and visualization to build an integrated understanding that is rigorous, detailed, and relevant for both theorists and device engineers.
1. Thermodynamic Perspective on Phase Transitions
1.1 First-order and Second-order Transitions
In statistical physics, a phase transition is said to be of the first order if the first derivative of the free energy with respect to an external parameter (such as temperature or field) is discontinuous. Conversely, a second-order (or continuous) phase transition has continuous first derivatives but discontinuous or divergent second derivatives.
Using Landau theory, the free energy of a system near a transition point can be expanded as:
$$
F(\psi) = F_0 + a(T) \psi^2 + b \psi^4 + c \psi^6 + \dots
$$
Here, $ \psi $ is the order parameter, and $ a(T) $ varies with temperature. The nature of the transition depends on the sign of $ b $:
- If $ a(T_c) = 0 $ and $ b > 0 $, the system undergoes a second-order transition, with $ \psi $ changing continuously from zero.
- If $ b < 0 $ and $ c > 0 $, the free energy develops a double-well structure, leading to a first-order transition with a discontinuous jump in $ \psi $.
| Transition Type | Order Parameter Behavior | Latent Heat | Hysteresis | Typical Examples |
|---|---|---|---|---|
| First-order | Discontinuous | Yes | Yes | Melting, VO$_2$ MIT |
| Second-order | Continuous | No | No | Superconductivity, Ferromagnetism |
1.2 Stability, Metastability, and Hysteresis
In a first-order transition, the presence of multiple minima in the free energy leads to metastable states. Transitions between these states require nucleation and may exhibit hysteresis — a hallmark of first-order behavior. This is particularly relevant for device operation where field-driven transitions can be used to induce switching.
2. Phase Transitions in Low-Dimensional and Quantum Materials
2.1 Gate-Tuned Quantum Phase Transitions in 2D FETs
Two-dimensional materials offer a platform to probe and control phase transitions via external parameters such as gate voltage, electrostatic doping, or vertical pressure. Examples include:
- Mott transitions in correlated materials like WSe$_2$ or twisted bilayer graphene, where Coulomb repulsion localizes carriers.
- Charge-density-wave (CDW) transitions in 1T-TaS$_2$ and NbSe$_2$, where periodic lattice distortions emerge.
- Superconducting transitions in FeSe/SrTiO$_3$ interfaces or doped MoS$_2$.
- Topological phase transitions under gating in WTe$_2$ or Bi bilayers.
These transitions can often be mapped using a free energy landscape similar to Landau theory, with gate voltage $ V_{GS} $ serving as a tunable parameter.
2.2 Mapping Transitions via Carrier Density
In analogy to thermal phase transitions, one can define a carrier-density-dependent free energy:
$$
F(n) = F_0 + \alpha(n - n_c)^2 + \beta(n - n_c)^4 + \dots
$$
Such a model predicts instabilities, bistability, and even hysteresis in electrical characteristics as observed in resistive switching, CDW sliding, or Wigner crystal formation.
3. Landau Theory and Negative Capacitance
3.1 Free Energy of a Ferroelectric System
A ferroelectric material near its Curie temperature can be modeled using the LGD expansion:
$$
G(P) = \frac{\alpha}{2} P^2 + \frac{\beta}{4} P^4 + \frac{\gamma}{6} P^6 - E P
$$
Here, $ P $ is the polarization, $ E $ is the electric field, and $ \alpha $, $ \beta $, $ \gamma $ are material-specific coefficients. For $ \alpha < 0 $, the free energy exhibits a double-well shape, indicating spontaneous symmetry breaking. The region between the wells has:
$$
\frac{d^2G}{dP^2} < 0 \Rightarrow C_{FE} < 0
$$
which corresponds to negative differential capacitance. However, this region is thermodynamically unstable unless stabilized by an external circuit.

3.2 Stabilization via Capacitance Matching
In a typical NC-FET structure, the ferroelectric layer is placed in series with the gate oxide and semiconductor channel. The effective capacitance becomes:
$$
\frac{1}{C_{total}} = \frac{1}{C_{FE}} + \frac{1}{C_{MOS}}
$$
When $ C_{FE} < 0 $ and $ |C_{FE}| \approx C_{MOS} $, the total capacitance $ C_{total} $ increases, leading to an amplified surface potential:
$$
\frac{d\phi_s}{dV_{GS}} > 1 \Rightarrow SS < 60~\text{mV/dec}
$$
However, achieving this condition in practice is nontrivial due to the constraints of stability, material defects, and domain dynamics.
4. Subthreshold Swing and Measurement Interpretation
4.1 Understanding Sub-60 mV/dec Behavior
The subthreshold swing (SS) in FETs is defined as:
$$
SS = \left( \frac{d\log I_D}{dV_{GS}} \right)^{-1}
$$
In ideal MOSFETs:
$$
SS_{min} = \ln(10) \cdot \frac{kT}{q} \approx 60~\text{mV/dec at 300K}
$$
In NC-FETs, the internal voltage amplification allows:
$$
SS < 60~\text{mV/dec}
$$
Yet, many researchers argue that this behavior is transient, not thermodynamically stable. Time-dependent polarization switching and incomplete stabilization in the negative curvature region may artificially create steep slopes.
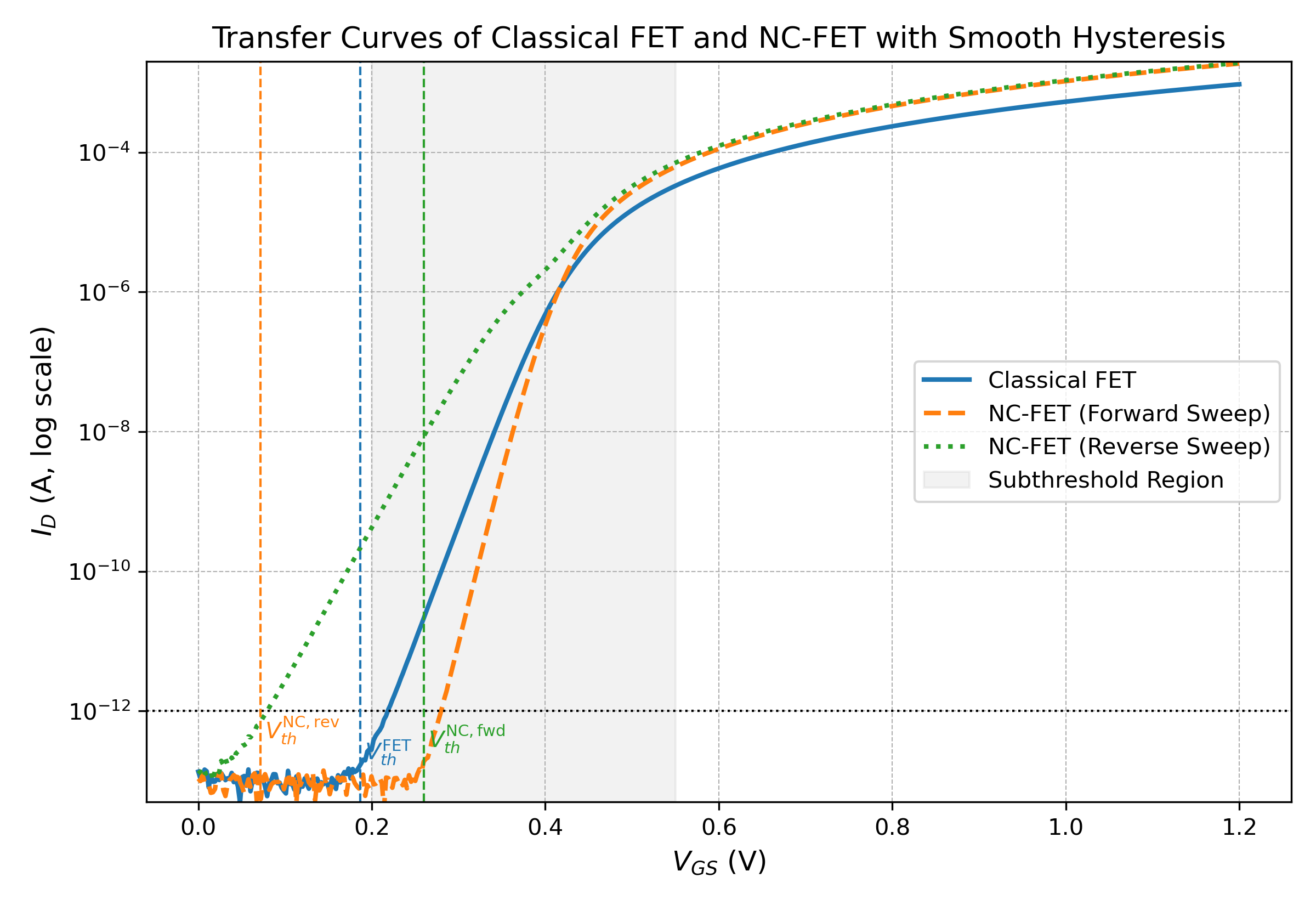
4.2 Scan Rate and Hysteresis Concerns
Measured transfer curves showing sub-60 mV/dec often vary with scan rate. Fast scans may capture polarization overshoot, while slow scans may reveal hysteresis or relaxation. This complicates the interpretation of “negative capacitance” as an equilibrium effect.
5. Critique and Theoretical Challenges
- Can negative capacitance be stabilized under quasi-static operation?
- Do domain dynamics and energy dissipation obscure equilibrium interpretation?
- Is the Landau framework sufficient, or is a microscopic model (e.g., DFT + polarization dynamics) needed?
- What are the impacts of film thickness, interface states, and non-idealities on $ C_{FE} $?
6. Outlook and Phase-Based Device Engineering
Despite challenges, the concept of harnessing phase transitions for electronic functionality is powerful and forward-looking. Emerging directions include:
- Mott-FETs based on correlated oxides or moiré systems
- Electrostatic topological switching using TMDs and Bi bilayers
- Van der Waals ferroelectrics for scalable NC-FETs
- Phase-coherent devices operating near quantum critical points
This suggests a shift from charge-centric control to phase-centric design in future nanoelectronics.
References
- Landau, L.D., Lifshitz, E.M. Statistical Physics.
- Salahuddin, S. & Datta, S. (2008). Nano Letters, 8(2), 405–410.
- Khan, A.I. et al. (2020). Nature Electronics, 3, 588–595.
- Zubko et al. (2011). Interface physics in complex oxide heterostructures. ARCM.
- Wang et al. (2021). 2D Materials and Phase Engineering. Nat. Rev. Mater.